Unraveling the Mysteries: 10 Favorite Conjectures and Open Problems in Mathematics

Mathematics has always been a subject that flirts with the unknown, inviting our curiosity to explore unsolved problems and unravel the mysteries hidden within its equations and theorems. Despite the tremendous advancements achieved over centuries, there are still several conjectures and open problems waiting to be cracked by intrepid mathematicians. In this article, we will venture into the realm of favorite conjectures and open problems in mathematics, inspiring you to ponder these mathematical puzzles and the potential breakthroughs they may unlock.

Hodge Conjecture

The Hodge conjecture, proposed by William Hodge in 1950, aims to relate specific cohomology groups of a smooth projective algebraic variety with Hodge structures to its cycles and classes. It remains one of the most prominent unsolved problems in algebraic geometry, perplexing mathematicians in their attempts to bridge the gap between these distinct mathematical entities.

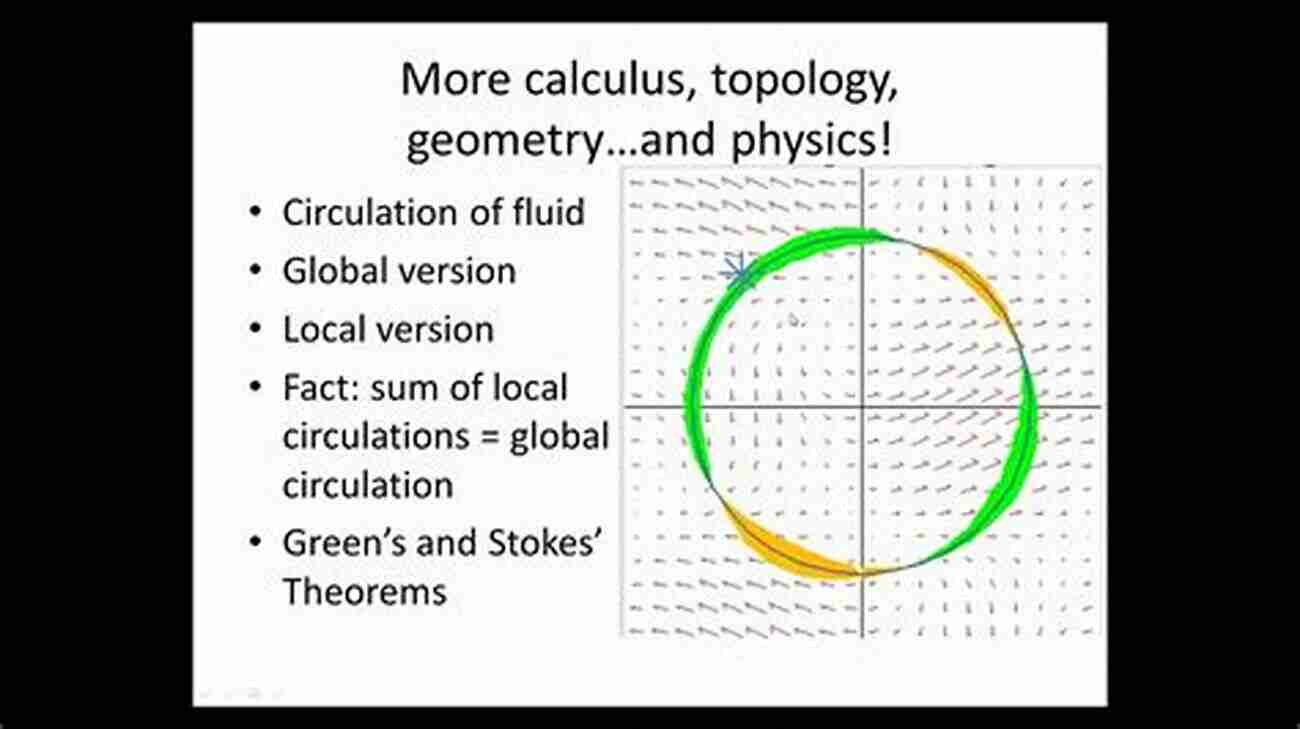
Riemann Hypothesis

First formulated by Bernhard Riemann in 1859, the Riemann Hypothesis delves into the complex world of prime numbers. It postulates that all non-trivial zeros of the Riemann zeta function lie on the "critical line" with real part 1/2. This conjecture is central to many fields, including mathematical analysis and number theory, and its resolution could have far-reaching consequences for cryptography and distribution of prime numbers.

Graph Theory: Favorite Conjectures and Open Problems - 2 (Problem Books in Mathematics)

by Teresa W. Haynes(1st ed. 2018 Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	6607 KB
Print length	:	287 pages
Screen Reader	:	Supported

FREE

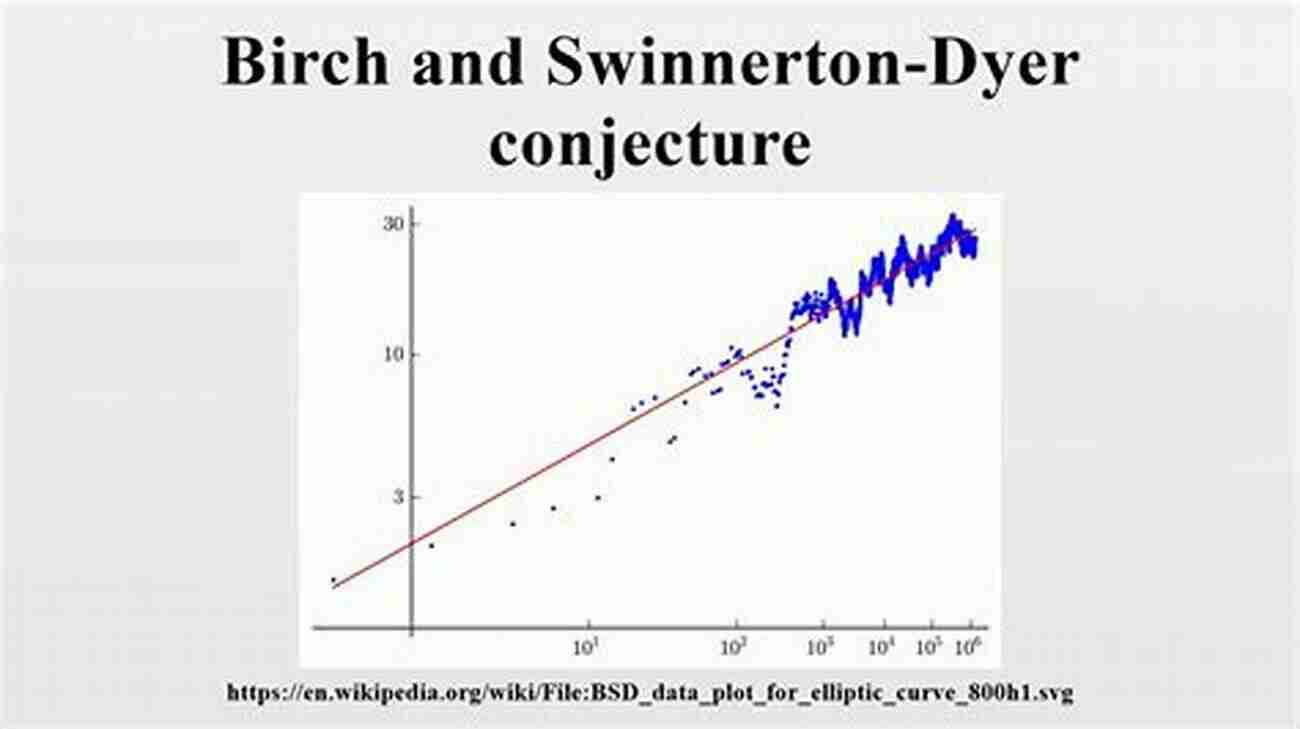
Birch and Swinnerton-Dyer Conjecture

The Birch and Swinnerton-Dyer conjecture, formulated in 1965, deals with the relationship between the number of rational points on an elliptic curve and the 'complex multiplication' of its associated L-series. It proposes that elliptic curves with a non-zero 'analytic rank' have an abundance of rational points. This conjecture remains an enigma, casting a captivating shadow over the study of elliptic curves and their arithmetic aspects.

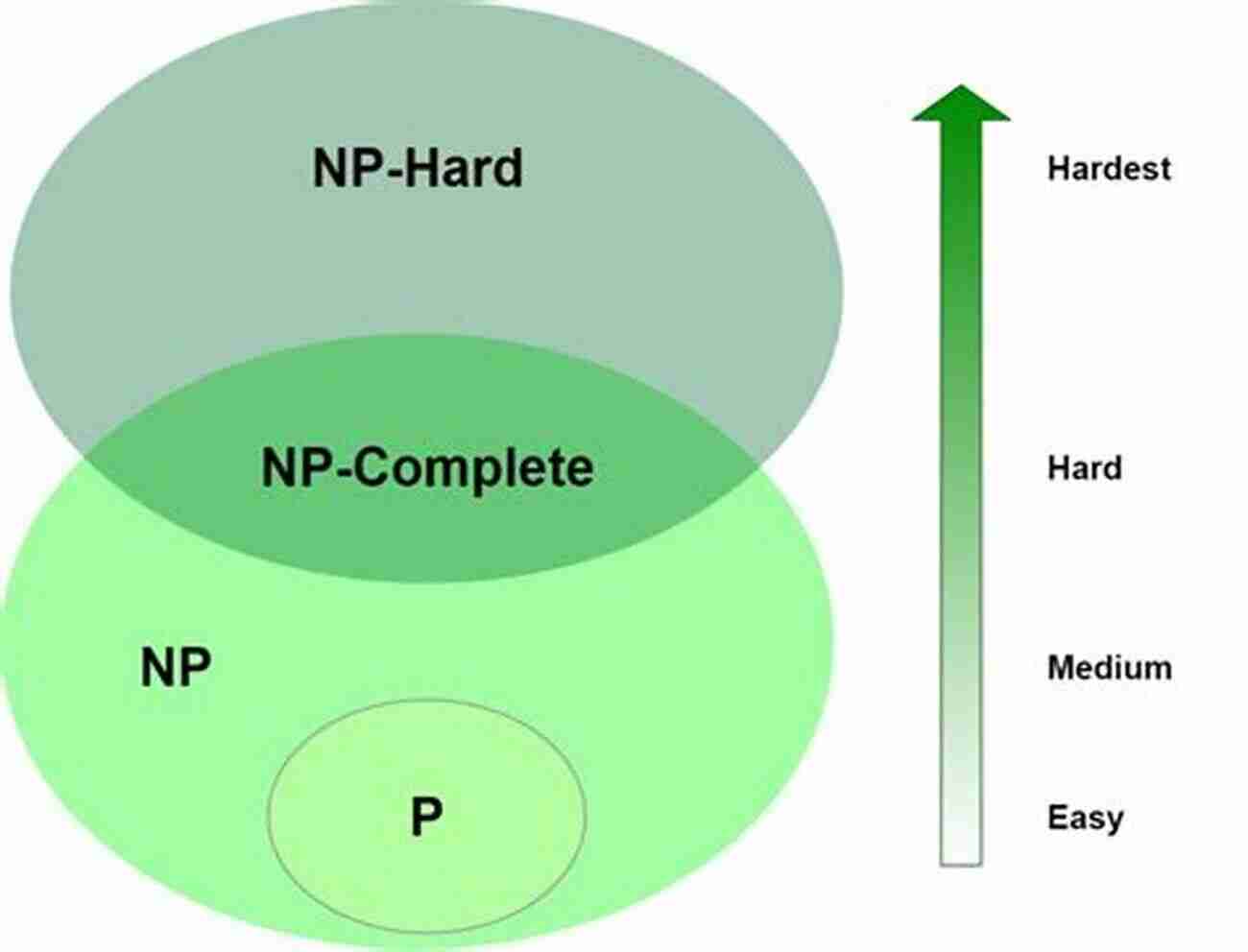
P versus NP Problem

The P versus NP problem poses a question fundamental to computer science and the theory of computational complexity. It investigates whether every problem for which a solution can be verified in polynomial time can also be solved in polynomial time. If P (problems solvable in polynomial time) is proven to be equal to NP (problems verifiable in polynomial time),then efficient solutions could be found for currently intractable problems, revolutionizing fields such as cryptography, optimization, and artificial intelligence.

Goldbach's Conjecture

One of the oldest unsolved problems in number theory is Goldbach's Conjecture, proposed by the German mathematician Christian Goldbach in 1742. The conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers. Despite extensive testing, no counterexamples have been found, but a rigorous proof still eludes mathematicians, locking this conjecture within the realms of mystery.

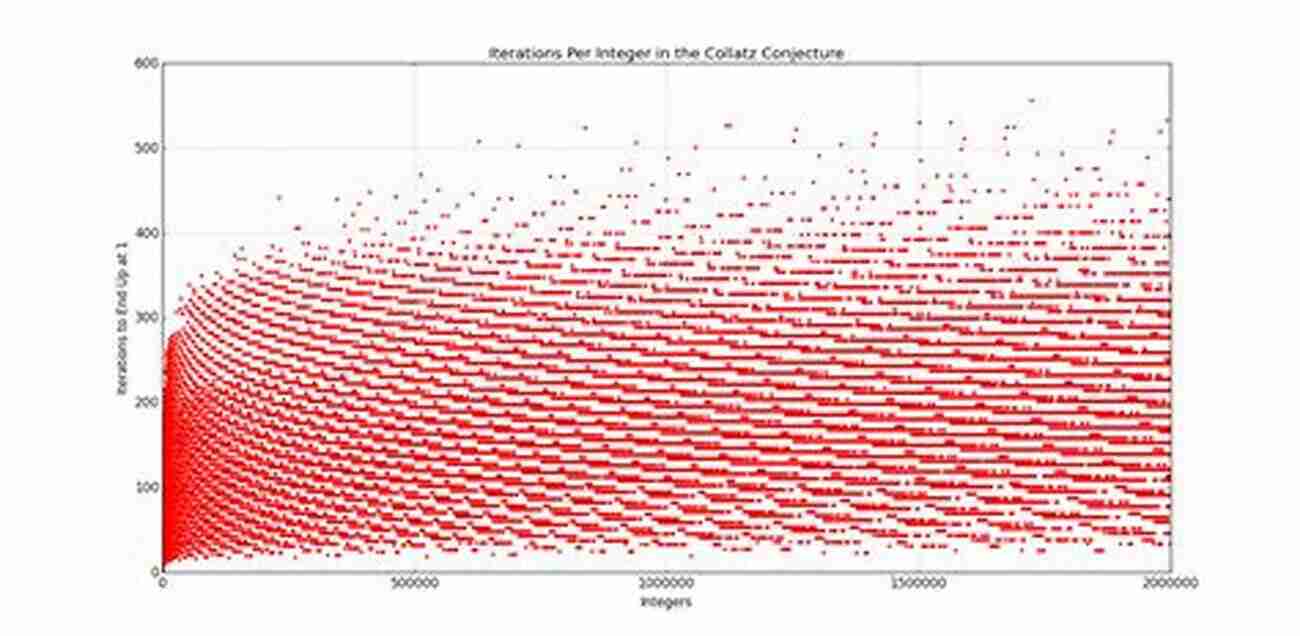
The Collatz Conjecture

The Collatz Conjecture, first introduced by German mathematician Lothar Collatz in 1937, is an intriguing numerical puzzle. It posits that, starting from any positive integer, if it is even, divide it by 2; if it is odd, multiply it by 3 and add 1. Repeat this process, and eventually, you will reach the number 1. Although extensively tested for smaller integers, the conjecture remains unproven for all numbers, posing a captivating challenge for mathematicians and enthusiasts alike.

Navier-Stokes Existence and Smoothness

The Navier-Stokes equations describe the behavior of fluid flow, playing a vital role in fields such as aerodynamics, climate modeling, and even the simulation of blood flow through arteries. The Navier-Stokes Existence and Smoothness problem focus on determining whether smooth solutions exist for these equations. While solutions are known for specific circumstances, proving the existence and smoothness of solutions for all possible situations remains an open and challenging problem in mathematical physics.

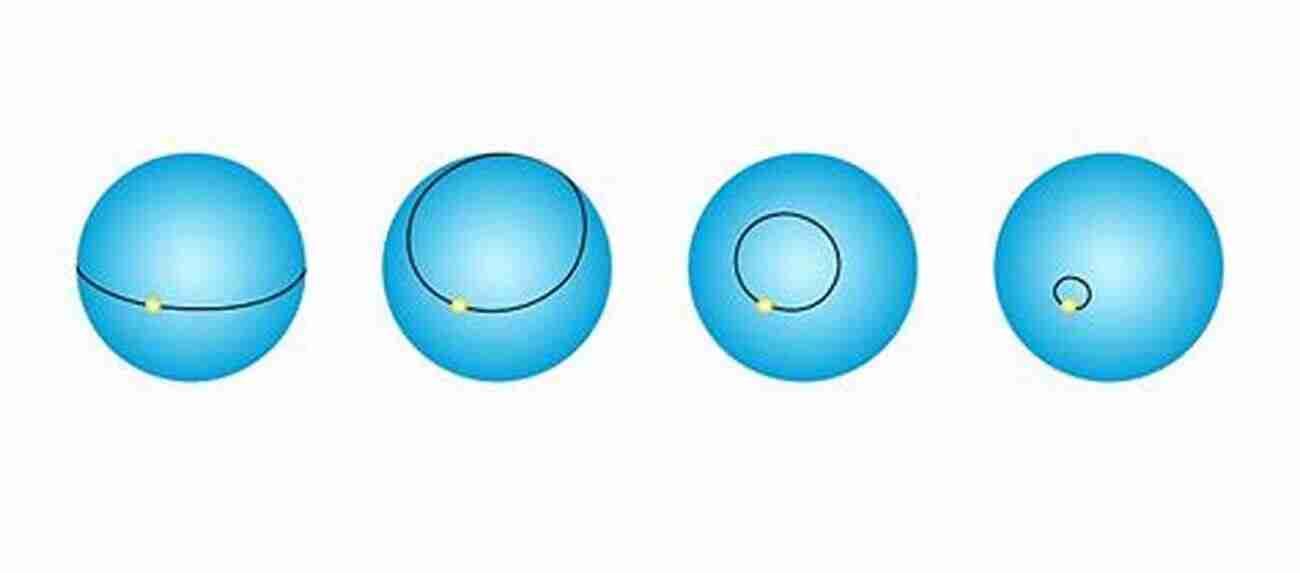
Poincaré Conjecture

The Poincaré Conjecture, named after French mathematician Henri Poincaré, deals with the topology of 3-dimensional spaces. It asserts that any simply connected, closed, and bounded three-dimensional manifold is homeomorphic to a sphere. This seemingly simple conjecture held mathematicians captive for over a century until finally proven by Grigori Perelman in 2003, marking a monumental milestone in mathematics and topology.

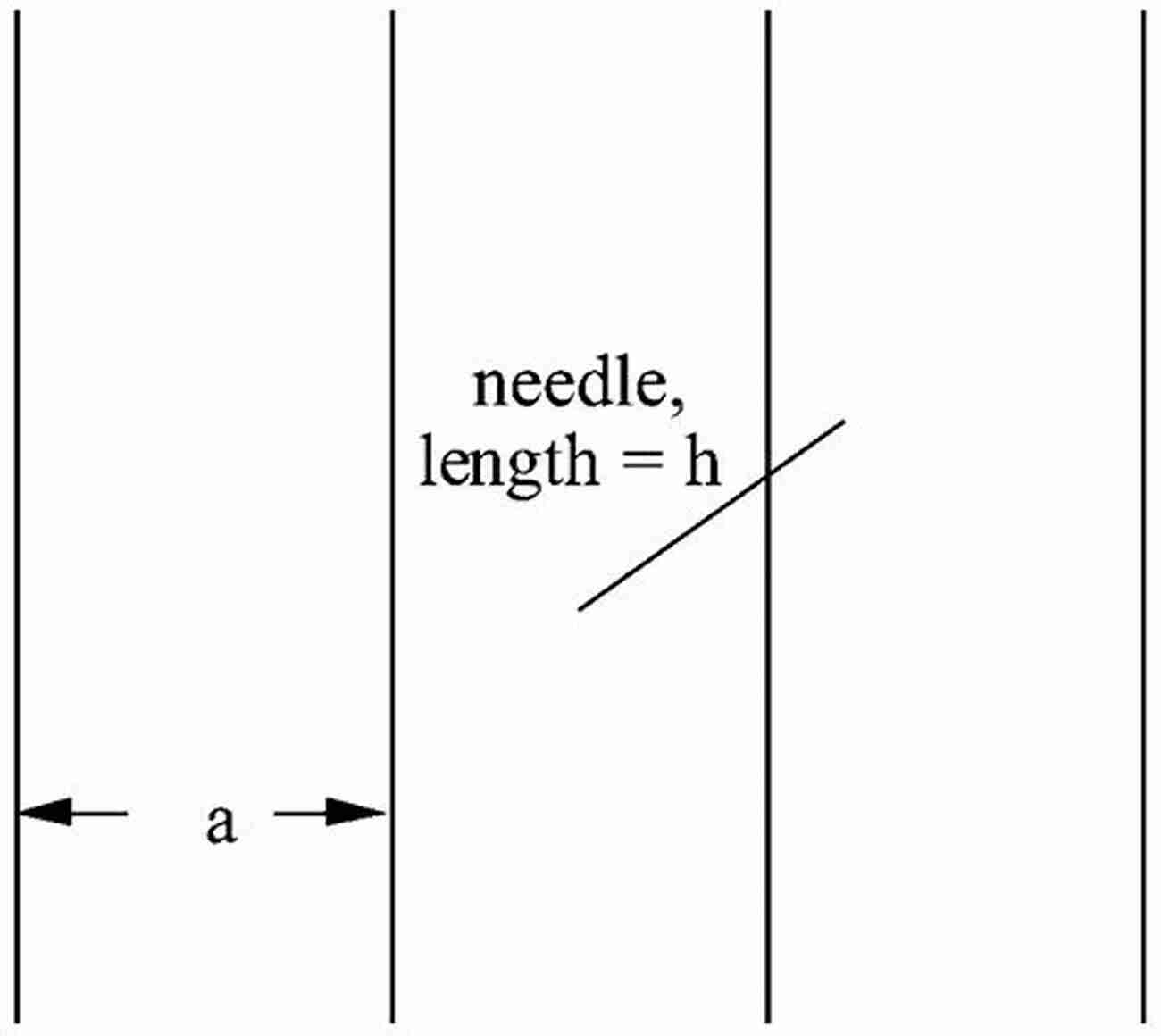
Buffon's Needle Problem

Buffon's Needle Problem, posed by Georges-Louis Leclerc, Comte de Buffon in the 18th century, is a thought experiment that explores the probability theory. It involves randomly dropping a needle of length L onto a plane, ruled with parallel lines separated by a distance D greater than L. The problem asks for the probability that the needle crosses one of the lines. This intriguing problem has led to new understandings in the mathematical fields of geometric probability, Monte Carlo simulations, and integral calculus.

Fermat's Last Theorem

One of the most notorious challenges in mathematics, Fermat's Last Theorem, consumed the minds of mathematicians for over three centuries before it was finally proven by Andrew Wiles in 1994. This theorem states that there are no three positive integers a, b, and c that satisfy the equation a^n + b^n = c^n for any integer value of n greater than 2. The proof involved deep connections between elliptic curves, modular forms, and Galois representations, highlighting the power of interweaving various areas of mathematics in solving complex problems.

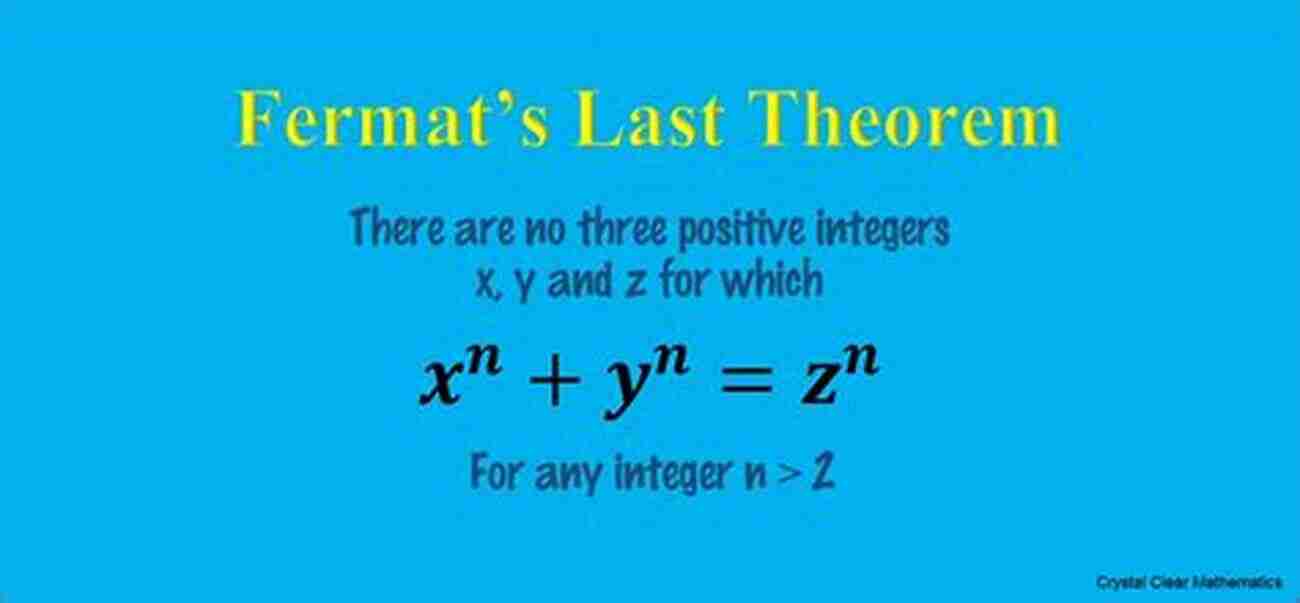
Mathematics continuously fuels our curiosity and challenges us to push the boundaries of human knowledge. The favorite conjectures and open problems discussed in this article represent just a fraction of the vast sea of unsolved puzzles waiting to be conquered. Whether it be unraveling the mysteries of prime numbers, exploring geometric topologies, or delving into fluid dynamics, mathematicians around the world continue their tireless efforts to crack these enigmas, inching closer to a deeper understanding of the universal language of numbers.

Graph Theory: Favorite Conjectures and Open Problems - 2 (Problem Books in Mathematics)

by Teresa W. Haynes(1st ed. 2018 Edition, Kindle Edition)

5 out of 5

Language	:	English
File size	:	6607 KB
Print length	:	287 pages
Screen Reader	:	Supported

FREE

This second volume in a two-volume series provides an extensive collection of conjectures and open problems in graph theory. It is designed for both graduate students and established researchers in discrete mathematics who are searching for research ideas and references. Each chapter provides more than a simple collection of results on a particular topic; it captures the reader’s interest with techniques that worked and failed in attempting to solve particular conjectures. The history and origins of specific conjectures and the methods of researching them are also included throughout this volume. Students and researchers can discover how the conjectures have evolved and the various approaches that have been used in an attempt to solve them. An annotated glossary of nearly 300 graph theory parameters, 70 conjectures, and over 600 references is also included in this volume. This glossary provides an understanding of parameters beyond their definitions and enables readers to discover new ideas and new definitions in graph theory.

The editors were inspired to create this series of volumes by the popular and well-attended special sessions entitled “My Favorite Graph Theory Conjectures,” which they organized at past AMS meetings. These sessions were held at the winter AMS/MAA Joint Meeting in Boston, January 2012, the SIAM Conference on Discrete Mathematics in Halifax in June 2012, as well as the winter AMS/MAA Joint Meeting in Baltimore in January 2014, at which many of the best-known graph theorists spoke. In an effort to aid in the creation and dissemination of conjectures and open problems, which is crucial to the growth and development of this field, the editors invited these speakers, as well as other experts in graph theory, to contribute to this series.